The problem goes like this

The solution is explained in the video solution below:
If you do not have Data pack to watch the video, you can even check out my slides and download it here 👇
Check out and download the solution slide 👇
Physics NET/GATE/JAM Competitive FREE materials
Quality Advanced Physics Resources over the Internet

The problem goes like this

The solution is explained in the video solution below:
If you do not have Data pack to watch the video, you can even check out my slides and download it here 👇
Check out and download the solution slide 👇
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
The polynomials arise in:
probability, such as the Edgeworth series;
✅in combinatorics, as an example of an Appell sequence, obeying the umbral calculus;
✅in numerical analysis as Gaussian quadrature;
✅in physics, where they give rise to the eigenstates of the quantum harmonic oscillator;
✅in systems theory in connection with nonlinear operations on Gaussian noise.
✅in random matrix theory in Wigner–Dyson ensembles.
Here’s a Quick note on Hermite Polynomial and Hermite Functions. This is pretty much what you will need for your competitive exams and interviews.
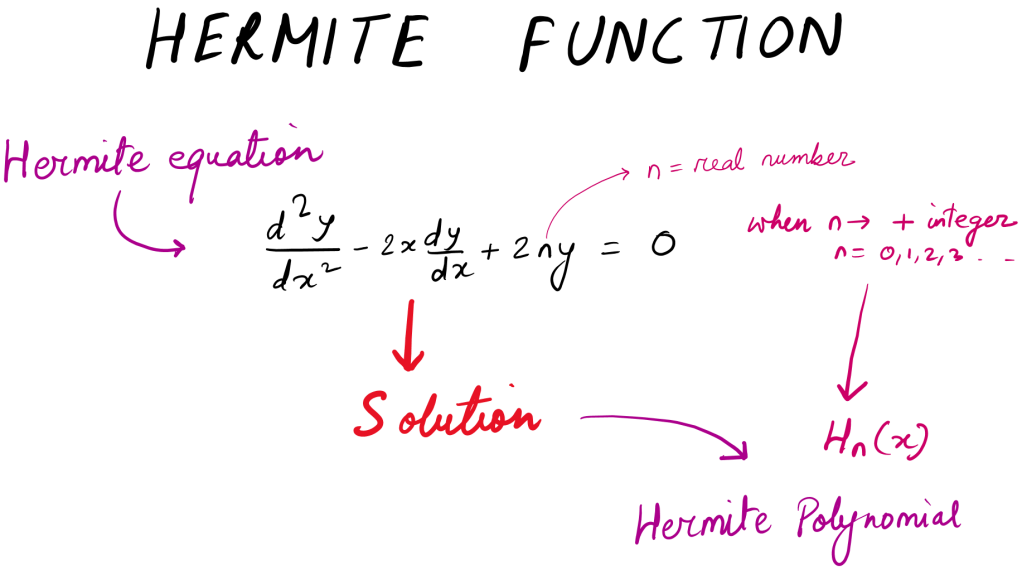
The video solution is presented below:
If you are interested in the PDF version of the notes:

The problem goes like this:

The solution is explained in the video solution below:
If you do not have Data pack to watch the video, you can even check out my slides and download it here 👇
Check out and download the solution slide 👇

The problem goes like this:

The solution is explained in the video solution below:
If you do not have Data pack to watch the video, you can even check out my slides and download it here 👇
Check out and download the solution slide 👇